Unit Circle and Its Applications

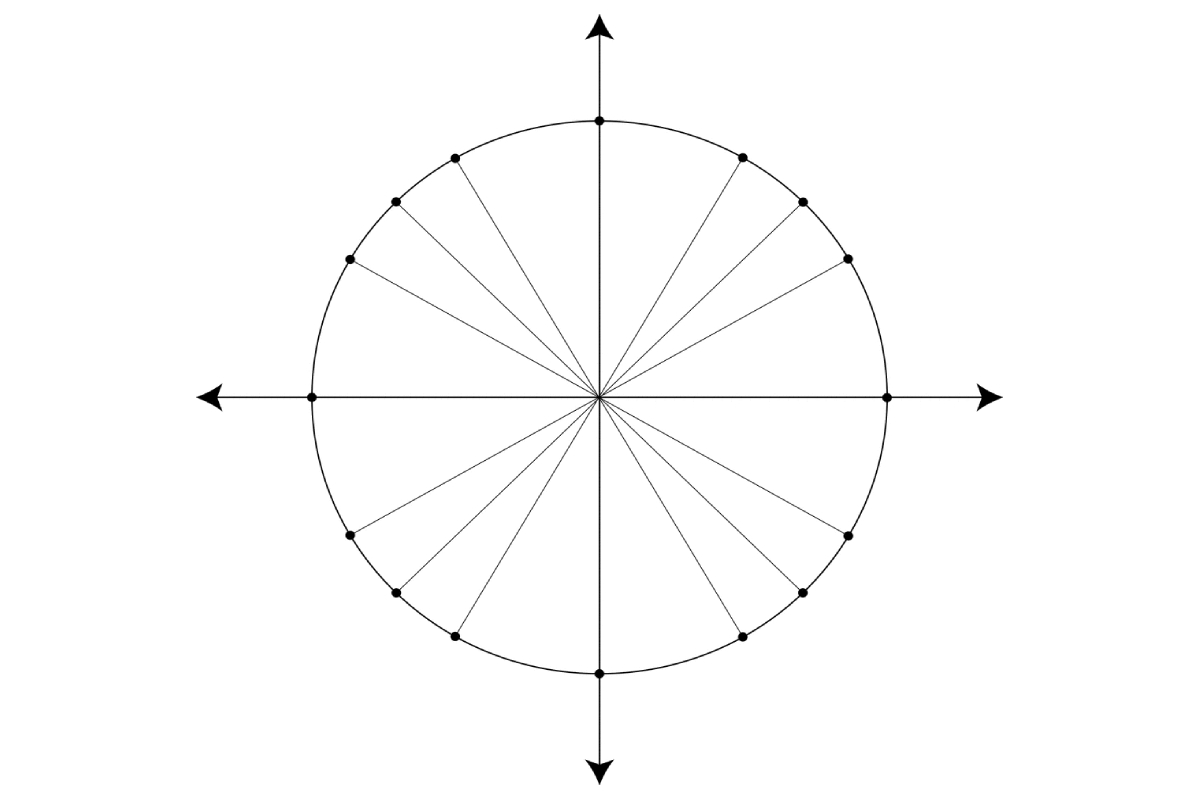
Unit Circle and Its Applications – In mathematical terms, a unit circle is a circle that has a radius of one unit and whose centre is located at the origin. Unit circle is generally represented in the cartesian coordinate plane and is algebraically represented with two variables x and y. Since it is a circle with a radius of one unit, it is simple to understand. We take its help to learn about various angles and lengths. It is used to calculate trigonometric functions, namely sin(θ), cos(θ), tan(θ), cot(θ), cosec(θ), and sec(θ). Let us understand in detail how unit circles help us in trigonometry.

The unit circle continues to be one of the most powerful tools in mathematics because it visually represents trigonometric values and their relationships. Beyond basic trigonometry, the unit circle’s real strength lies in its ability to simplify complex equations and explain periodic phenomena. For students struggling with memorizing trigonometric ratios, the unit circle provides a clear, geometric understanding of how sine and cosine change as an angle moves around a circle. This not only makes learning easier but also helps build a strong foundation for higher mathematical concepts.

Using the Unit Circle in Complex Numbers

The unit circle helps visualize complex numbers in polar form. Each point on the circle represents a complex number with magnitude 1. This concept is widely used in electrical engineering, filters, and control systems, making the unit circle essential for advanced mathematics.

Another important application of the unit circle is in the study of rotational symmetry and periodic functions. Every complete rotation (360° or 2π radians) brings the point back to its original position, which mirrors the periodic nature of many real-life systems. For instance, clocks, seasonal changes, waves, and circular motions all reflect the same periodic principles illustrated by the unit circle. Understanding how these values repeat helps students grasp the behavior of sine and cosine waves, which are crucial in physics, communication systems, and engineering.

Trigonometric Functions from Unit Circle

In advanced mathematics, the unit circle plays a critical role in complex number theory. When complex numbers are expressed in polar form, their magnitude and angle correspond directly to points on the unit circle. Multiplying complex numbers involves adding angles, which becomes easier to visualize using the circle. This concept is used heavily in electrical engineering, especially in AC circuits where alternating current cycles can be visualized using circular rotation on the complex plane.

You all might be aware of what trigonometry is. If not, let us understand now. It is a branch of mathematics that deals with specific angles and lengths of a triangle. Trigonometry is believed to have its origin from the Hellenistic world during the third century BC. It is extremely important for all of us to learn about trigonometry because many of the natural structures and shapes of the Earth resemble triangles. It plays an important role in areas of engineering, oceanography, electronics, biology, chemistry, game development, and the list continues. Now, a question will arise in your mind about how unit circle has relevance in trigonometry. Let us understand how.

How does Unit Circle help in Deriving Trigonometric Functions?

As we all know, a unit circle is formed with its centre at the point of origin that is at (0,0) and whose radius is one. Thus, the circumference of a unit circle is 2π. An arc of the unit circle has the same length as that of the measure of the central angle that intercepts that arc. The radius of the unit circle is one, so the trigonometric functions sine, cosine, and tangent have special relevance for the unit circle. We can find these trigonometric functions by applying the Pythagoras theorem. Let us take a right-angled triangle and understand how.

The radius present inside the circle of the right-angled triangle represents the hypotenuse. Let x be the altitude and y be the base. Now, we have a triangle with sides x unit, 1 unit, and y unit. If we apply the Pythagoras theorem, we get sin θ = y/1 and cos θ = x/1. Now, if we divide sin θ by cos θ, we arrive at the value of tan θ. Cosecant (cosec), secant (sec), and cotangent (cot) can also be easily obtained as these trigonometric functions are the reciprocal of sin, cosine (cos), and tangent (tan) respectively.

Understanding Pythagorean Identities Using Unit Circle

We have already discussed the Pythagoras theorem before. By definition, it states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the other two sides of the triangle.

Formula: x.x + y.y = z.z

Where, z = hypotenuse of right triangle

y = base of the right triangle

x = altitude of the right triangle.

With the help of a unit circle, the three important Pythagorean identities of trigonometric ratios can easily be proved and understood. The three Pythagorean identities in trigonometry are discussed below:

1. sin.sinθ + cos.cosθ = 1
2. sec.secθ = 1 + tan.tanθ
3. cosec.cosecθ = 1 + cot.cotθ

Unit Circle in Complex Plane

A complex number is the summation of a real number and an imaginary number. A complex plane in mathematics is a plane formed by an entire set of complex numbers. A unit circle has all complex numbers of absolute values as 1. Thus, it has the equation of |z| = 1. The unit circle can be seen as unit complex numbers in a complex plane that is the set of complex numbers z given by the form,

Z = e^it = cos t + i sin t = cis(t).

If you want to learn more about unit circle and trigonometry in a fun and interesting way, visit Cuemath.

Unit Circle in Signal Processing

In digital signal processing, the unit circle helps represent digital filters and determine stability. Engineers use unit circle plots to understand how signals behave and how to design efficient audio, communication, and image-processing systems.

The unit circle is also central to Fourier analysis, a mathematical technique used to break down complex waveforms into simpler sinusoidal components. Applications include audio engineering, telecommunications, signal processing, and even medical imaging technologies like MRI. The idea that any repeating signal can be represented as a combination of sine and cosine waves originates from the geometry of the unit circle.

In summary, the unit circle isn’t just a mathematical diagram — it is a universal model for understanding cycles, rotations, waves, and complex mathematical relationships. Its applications stretch across mathematics, physics, engineering, and computer science, making it one of the most important concepts students can master.